When we looked at searching algorithms in 3-5, the “divide and conquer” strategy of the binary search dramatically reduced the number of comparisons needed to find the search key. In a similar way, when sorting data, if we can continuously subdivide a large data set into smaller sets, sort each of those smaller sets, and then recombine the smaller sorted sets together, this can greatly improve sorting performance. Recursive sorting techniques such as the quicksort work exactly like this!
Quick Sort
The quick sort was invented in 1962 and is actually considered one of the top 10 algorithms of the 20th century! The quick sort works by partitioning (i.e., dividing) an array using a specially chosen element called a pivot.
There are many different ways that a pivot element can be selected, the simplest is to choose the middle element of the array as the pivot.
To partition the array, we rearrange all of the elements such that those that are smaller than the pivot value (P) appear on the left and those that are larger appear on the right. Elements that are equal to the pivot can end up in either side of the array, it won’t matter. Partitioning may not split the array exactly in half, we may end up with more items on the left or right of the pivot.
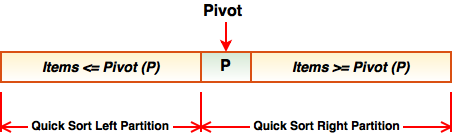Once partitioning is complete, we use exponential recursion to quickSort() the subarray of items to the left of the pivot and from the pivot to the right.
As with recursiveBinarySearch(), I’m going to provide a public method that requires no parameters and simply calls the private recursive quickSort() method, passing in the index of the first and last element of the array to start with. This way, we are hiding details about indices within the QuickSort class.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
// PUBLIC method to start the private recursive quickSort() // and pass in the first and last index of the data array. public void quickSort( ) { quickSort( 0, data.length - 1 ); } // PRIVATE recursive method to perform the quick sort, // requires left and right indices (internal details). private void quickSort(int leftIndex, int rightIndex) { // base case: if subarray size is 1, then it's sorted if ( rightIndex - leftIndex <= 0 ) return; // Otherwise, there are 2 or more elements in this subarray else { // Partition the subarray int indexOfPivot = partitionIt( leftIndex, rightIndex ); // Sort the left side quickSort( leftIndex, indexOfPivot - 1 ); // Sort the right side quickSort( indexOfPivot, rightIndex ); } } |
Every recursive algorithm requires a base case to stop recursion. In this case, if the quickSort() method is passed indexes of a (sub)array that indicate that there is only one item in the array then we stop.
Otherwise, we partition the (sub)array and then call the quickSort() method again twice recursively to sort the subarray of items that are less than (i.e., to the left of) the pivot element, and those that are greater than (i.e., to the right of) the pivot.
Partitioning
Since the partitionIt() method is only useful to our quickSort() method, I’ve made it a private helper method. Here’s the code for it:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
// helper method to partition the array private int partitionIt(int leftIndex, int rightIndex) { int pivotValue = data[(leftIndex + rightIndex) / 2]; while ( leftIndex <= rightIndex) { while ( data[leftIndex] < pivotValue ) leftIndex++; while ( data[rightIndex] > pivotValue ) rightIndex--; if ( leftIndex <= rightIndex ) { swap( leftIndex, rightIndex ); leftIndex++; rightIndex--; } } return leftIndex; } |
As described earlier, the partitionIt() method selects the middle element in the (sub)array to be the pivotValue. As long as the leftIndex is actually to the left of (i.e., <=) the rightIndex, the outer loop will iterate. Using two inner while loops a linear search is made from the left to the right looking for the first element that is greater than or equal to the pivotValue. The leftIndex index will point to this element. With a second inner loop, it then does a linear search from the right to the left looking for the first element that is less than or equal to the pivot. The rightIndex index will point to this element.
Next, as long as the leftIndex has not crossed over the rightIndex in this process, we swap() the elements, then move the leftIndex and rightIndex one more position, and start another iteration of the outer while loop.
Once the outer while loop has terminated (i.e., our leftIndex and rightIndex have crossed), we will have a (sub)array where items smaller than the pivotValue are on the left side of the (sub)array, and those that are larger are on the right.
The partitionIt() method returns the index of the pivot value (leftIndex) back to the quickSort() method. This is used by quickSort() to recursively sort the elements to the left and right of the pivotValue. The pivot is in its correct place relative to the other elements in the array.
You Try!
- Using the BubbleSort class (from 3-7) as a model, and the quick sort methods explained above, create a QuickSort and QuickSortTest class. Use your classes to time the quick sort against RANDOM, ASCENDING, and DESCENDING data sets of 100,000 elements. Record your results.
- How many times faster is quick sort than selection sort on 100,000 random integers?
- Time the quick sort again with 1,000,000 and 10,000,000 RANDOM integers. Record your results.
- How long do you think it would take for selection sort to sort 1,000,000 RANDOM integers?
- If recursive search algorithms are so much faster than sequential ones, why would we ever use a sequential algorithm? Aren’t sequential algorithms a waste of time? Discuss the pros and cons.