You’ve seen that the Arrays class and ArrayList collection include handy methods to search for the index of an item within a 1D array or ArrayList object, respectively. As Java programmers it’s important to know how to use these Java API methods. However, as computer scientists, it’s even more important that we understand how to write our own search methods from scratch. That’s what we’ll tackle today!
Linear Search
A linear search works as its name implies, it searches for an item (called a key value) starting from the first element in a data structure and proceeds linearly (i.e., in order) through all the elements until the key value is either found or we reach the last element. Linear search is the simplest, and most brute force, searching algorithm there is. Here is a class to demonstrate:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 |
import java.util.Arrays; import java.util.Random; public class LinearSearch { private int[] data; // Create array of given size and fill with random integers public LinearSearch( int size ) { data = new int[ size ]; Random generator = new Random(); // fill array with random 2-digit integers in range 10-99 for ( int i = 0; i < size; i++ ) data[ i ] = 10 + generator.nextInt( 90 ); } // Performs an iterative linear search for the searchKey in the array. // Returns the index where searchKey is found, or -1 otherwise. public int iterativeLinearSearch( int searchKey ) { // loop through array sequentially for ( int index = 0; index < data.length; index++ ) if ( data[ index ] == searchKey ) return index; // return index of integer return -1; // integer was not found } // This is not actually a recursive method. It is a PUBLIC method that // calls the PRIVATE recursiveLinearSearch() method passing in the index // of the first element of the data array to search. This way, the user does // not need to worry about internal details like indices. public int recursiveLinearSearch( int searchKey ) { return recursiveLinearSearch( searchKey, 0 ); } // This PRIVATE recursive method performs a linear search for searchKey at the // index provided. It returns the index where searchKey is found, or -1 otherwise. private int recursiveLinearSearch( int searchKey, int index ) { // Left as an exercise for YOU! return -1; } // Returns a String of all elements in the array public String toString() { return Arrays.toString( data ); } } |
The code above defines a LinearSearch class that encapsulates an array of random integer values (line 6) called data. The constructor allows outside code to specify how many random elements should be in the array. Lines 20 to 27 implement the linear search algorithm using an iterative (for loop) approach. This method takes a searchKey as a parameter and returns the index of the first occurrence of that key in the array, or -1 if a match is not found. Finally, the toString() method uses the static toString() method of the Arrays class to display the contents of the encapsulated data array. Ignore the recursiveLinearSearch() methods for now, more on these in the exercises today.
Going back to the constructor, notice the use of the Random class (imported from java.util). So far we’ve been using Math.random() to generate floating-point values and then simple arithmetic and casting to produce random integers within a particular range. The Random class provides convenient methods to generate any random primitive data type; for example, nextInt(), nextDouble(), and nextBoolean() – please consult the Java API for full details.
The nextInt() method call on line 15 returns a random integer between 0 (inclusive) and the parameter 90 (exclusive). By adding 10 to this I’m effectively shifting the range of random values from 0 to 89 to 10 to 99. This is just a design decision I’ve made to demonstrate how to shift the range.
Here is a test class to demonstrate the LinearSearch class:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
import java.util.Scanner; public class LinearSearchTest { public static void main( String args[] ) { int searchKey; int foundIndex; Scanner input = new Scanner( System.in ); // create 10 element, random array and display it LinearSearch searchArray = new LinearSearch( 10 ); System.out.println( searchArray ); // print array // get search key from user System.out.print( "Please enter an integer search key (-1 to quit): " ); searchKey = input.nextInt(); // repeatedly input a search key; -1 terminates the program while ( searchKey != -1 ) { // perform linear search for the key foundIndex = searchArray.iterativeLinearSearch( searchKey ); if ( foundIndex != -1 ) System.out.println( "Integer " + searchKey + " was found at index " + foundIndex + "." ); else System.out.println( "Integer " + searchKey + " was not found." ); System.out.print( "Please enter an integer value (-1 to quit): " ); searchKey = input.nextInt(); } } } |
[23, 17, 51, 45, 19, 74, 28, 28, 87, 42]
Please enter an integer search key (-1 to quit): 51
Integer 51 was found at index 2.
Please enter an integer search key (-1 to quit): 99
Integer 99 was not found.
Please enter an integer value (-1 to quit): -1
Binary Search
When a data set is in a random order the linear search is the only way to search for a key. However, when data is in sorted order there is a much more efficient algorithm we can use called the binary search.
The binary search works by using a “divide and conquer” approach:
- Define two indexes, low = 0, and high = index of the last element of the data.
- Calculate the index of the middle element = (low + high) / 2.
- If the middle element matches the key, return the middle
- If the key is greater than the middle element, set low = middle + 1.
- If the key is less than the middle element, set high = middle – 1.
- If the low index becomes greater than the high index, return -1 because the search has failed to find a match.
- Go back to step 2.
Let’s say we are looking for the key value 10 in an array of 10 integers:
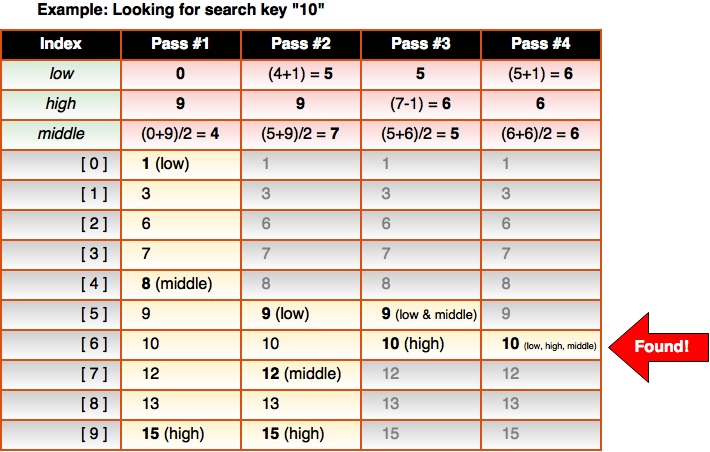
By changing the low and high indexes you can see that the binary search methodically cuts the number of elements to be searched in half. For very large arrays this can make a huge difference over linear search. Note that the calculation for middle uses integer division ( / ), so the remainder is simply truncated (not rounded).
In the case where the search key does not exist (for example, if the key was 11), we would have a situation where the low index exceeds the high index like so:
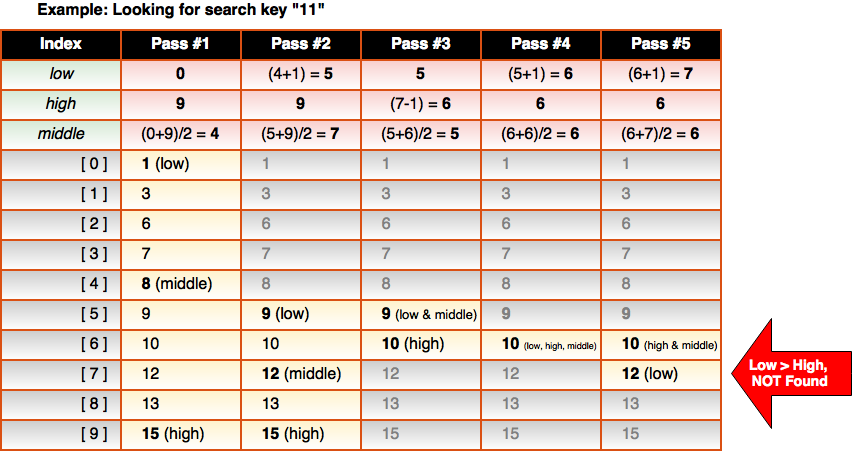
Let’s look at a BinarySearch class:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 |
import java.util.Arrays; import java.util.Random; public class BinarySearch { private int[] data; // create array of given size and fill with sorted random integers public BinarySearch( int size ) { data = new int[ size ]; Random generator = new Random(); // fill array with random 2-digit integers in range 10-99 for ( int i = 0; i < size; i++ ) data[ i ] = 10 + generator.nextInt( 90 ); // Put the array in numeric order Arrays.sort( data ); } // This is not actually a recursive method. It is a PUBLIC method that // calls the PRIVATE recursiveBinarySearch() method passing in the index // of the first and last item of the data array. This way, the user does // not need to worry about internal details like indices. public int recursiveBinarySearch( int searchKey ) { return recursiveBinarySearch( searchKey, 0, data.length -1 ); } // This PRIVATE recursive method performs a binary search for searchKey // between the low and high indices provided. It returns the index where // searchKey is found, or -1 otherwise. private int recursiveBinarySearch( int searchKey, int low, int high ) { // There are no elements left to be searched, searchKey not found. if (low > high) { return -1; } int middle = ( low + high ) / 2; // Display progress of current search (for demonstration only!) System.out.print( searchProgress( low, middle, high ) ); // Match! Return the index. if (searchKey == data[middle]) { return middle; } // The searchKey must be in the first half of the data, search there. else if (searchKey < data[middle]) { return recursiveBinarySearch( searchKey, low, middle - 1 ); } // The searchKey must be in the second half of the data, search there. else { return recursiveBinarySearch( searchKey, middle + 1, high ); } } // Performs an iterative binary search for the searchKey in the array. // This method only requires the searchKey, and returns the index where // searchKey is found, or -1 otherwise. public int iterativeBinarySearch( int searchKey ) { // Left as an exercise for YOU! return -1; } // helper method to produce a string showing the range being searched and the current middle. private String searchProgress( int low, int middle, int high ) { String result = ""; // output spaces for alignment for ( int i = 0; i < low; i++ ) result += " "; // output elements remaining to the searched for ( int i = low; i <= high; i++ ) result += data[ i ] + " "; result += "\n"; // next line, output spaces for alignment for ( int i = 0; i < middle; i++ ) result += " "; result += "*\n"; // indicate current middle with an asterisk (*) return result; } // Returns a String of all elements in the array and indicates the middle element with a * public String toString() { return searchProgress( 0, (data.length - 1) / 2, data.length - 1 ); } } |
Because binary search requires sorted data to work, line 18 calls the Arrays.sort() method to sort the random integers. The rest of the BinarySearch class is structured similarly to the LinearSearch class we discussed earlier. The searchProgress() helper method is used to display the range of elements in the array that are included in the current stage of the search with an asterisk (*) under the current middle element.
Remember when we talked about recursive methods I told you that some algorithms are naturally recursive? Binary search is one of them so I’ve chosen to implement it using a recursive method! You’ll note that there are two methods called recursiveBinarySearch(). The public one is actually not recursive at all. It allows outside code to start a binary search without having to pass in the index of the first element (0) – after all, this is an internal detail that a user should not have to worry about. The public method calls the private one, which actually performs the binary search recursively and returns the index of the searchKey if found, or -1 otherwise.
There are two base cases: (lines 34 to 36) if the low index > high index then the key was not found, and (line 44 to 46) if the key == the middle element then the key was found. There are two recursive cases as well, one that repeats the binary search on elements above the current middle element, and one that searches elements below it.
The BinarySearchTest class is nearly identical to LinearSearchTest:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
import java.util.Scanner; public class BinarySearchTest { public static void main( String args[] ) { int searchKey; int foundIndex; Scanner input = new Scanner( System.in ); // create 15 element, sorted array and display it BinarySearch searchArray = new BinarySearch( 15 ); System.out.println( searchArray ); // get search key from user System.out.print( "Please enter an integer value (-1 to quit): " ); searchKey = input.nextInt(); // repeatedly input a search key; -1 terminates the program while ( searchKey != -1 ) { // perform binary search for the key foundIndex = searchArray.recursiveBinarySearch( searchKey ); if ( foundIndex != -1 ) System.out.println( "Integer " + searchKey + " was found at index " + foundIndex + ".\n" ); else System.out.println( "Integer " + searchKey + " was not found.\n" ); System.out.print( "Please enter an integer value (-1 to quit): " ); searchKey = input.nextInt(); } } } |
Try the code above and experiment with different search keys. Sometimes there can be duplicate data values in the search array — which one does binary search find?
Which Algorithm is Better?
It depends! The linear and binary search both produce the same result but they do so in very different ways. Which algorithm is the “best” depends on several factors. The advantages of the linear search are that it is very simple to code (and read!) and does not require the data being searched to be in order, which is often the case in the real world. On the other hand, if the data is sorted and especially if there are many elements, the superior performance of the binary search is clear.
For example, let’s say we have an array of n = 1,000,000 elements. Using linear search, if the key exists in the array, we will find it after ~500,000 comparisons (i.e., n/2) on average. With binary search the key will be matched in ~20 comparisons (i.e., log2n) on average because half of the elements can be eliminated from the search on each pass. Next time we’ll get into the details of how to compare the efficiencies of different algorithms.
You Try!
- Let’s say we have an ordered (sorted) array of many elements, but some of the elements repeat. Using a linear search algorithm, if we searched for an element that appeared more than once in the array which duplicate value would be found first? Now, consider the same question using a binary search. Would it always find the first of the duplicate elements? Explain. Try to verify your hypothesis using the BinarySearchTest program.
- You’ll note in the LinearSearch class that I included an empty private recursiveLinearSearch() Complete the code for this method and revise the LinearSearchTest class to demonstrate that your method works. Hint: There will be 2 base cases and one recursive case in your code. Remove line 43: return -1; This was only included as a placeholder so that the code would compile.
- You’ll note in the BinarySearch class that I included an empty iterativeBinarySearch(). Complete the code for this method and revise the BinarySearchTest class to demonstrate that your method works. Remove line 64: return -1; This was only included as a placeholder so that the code would compile.