2-9 Enhancing the Fraction Class

Before we move on to inheritance and polymorphism let’s solidify our knowledge of objects, methods, and references by enhancing the Fraction class one last time.

Inverting a Fraction Object

When working with fractions in math we sometimes need to invert them; for example, when dividing fractions we invert and multiply. This may seem like a trivial thing to do but there is a trick to it in programming. Consider this attempt to swap the values in two variables:

num = den;
den = num;

1 2	num = den; den = num;

This results in a logic error. On the first line we will lose the value of num when it is overwritten by den, then the second line will overwrite den with the same value. In other words, after these two lines execute they will both contain the value from den. In order to swap values successfully in programming we need a temporary variable to store one of the values.

    public void invert() {
        if ( num == 0 ) {
            System.err.println( "Attempt to invert Fraction with 0 numerator, setting to 1 by default." );
            num = 1;
        }
        int temp = num;     // make a copy of numerator
        num = den;          // overwrite numerator with denominator value
        den = temp;         // overwrite denominator with temporary copy of numerator
    }

public void invert() {

if ( num == 0 ) {

System.err.println( "Attempt to invert Fraction with 0 numerator, setting to 1 by default." );

num = 1;

}

int temp = num; // make a copy of numerator

num = den; // overwrite numerator with denominator value

den = temp; // overwrite denominator with temporary copy of numerator

}

Notice that I’ve also added some sanity checking at the start of this method to ensure that if the numerator is 0 it gets set to 1 before inverting. Here’s a sample interaction with this method:

> Fraction f = new Fraction( 0, 2 )
> System.out.println( f )
0/2
> f.invert()
Attempt to invert Fraction with 0 numerator, setting to 1 by default.
> System.out.println( f )
2/1

Comparing Fraction Objects

Earlier we learned that objects cannot be compared for equality using the == operator because this does not compare the contents of the objects but rather their memory addresses. The only way == would result in true is if two reference variables are pointing to the exact same object in memory.

With String objects we used the equals() method to compare the current String object with another String object passed in as a parameter. Let’s add an equals() method to our Fraction class.

For two Fraction objects to be equal does not necessarily mean that they have the same numerator and denominator. What matters is that their magnitudes are equal. We should be able to interact with our Fraction class like so:

> Fraction f1 = new Fraction( 2, 3 )
> Fraction f2 = new Fraction( 2, 3 )
> f1 == f2
false
> f1.equals( f2 )
true
> f2.equals( f1 )
true

So there are two parts to this solution. First we need a way (a method) to calculate the magnitude of a fraction as a floating-point number. In a previous exercise, you created a toDouble() method that we can use for this purpose:

    public double toDouble() {
        return (double) num / den ;
    }

public double toDouble() {

return (double) num / den ;

}

Using this method we can now write a Boolean equals() method to compare the magnitude of the current Fraction object with a parameter Fraction object.

    public boolean equals( Fraction other ) {
        return toDouble() == other.toDouble();
    }

public boolean equals( Fraction other ) {

return toDouble() == other.toDouble();

}

The second line calls the toDouble() method in the current Fraction object and compares its result with the result returned from the toDouble() method in the other (parameter) Fraction object. The result of this expression is returned by our equals() method.

Reducing Fraction Objects

Reducing fractions is another common operation on fractions. To reduce a fraction one must find the GCD of the numerator and denominator, then divide both by the GCD. Fortunately in 2-3 I challenged you to write a recursive GCD method. Let’s cut and paste the solution to that challenge into our Fraction class:

    private int gcd( int a, int b ) {
        if ( b == 0 ) { 
            return a;
        }
        else {
            return gcd( b, a % b );  
        }
    }

private int gcd( int a, int b ) {

if ( b == 0 ) {

return a;

}

else {

return gcd( b, a % b );

}

This time, I’ve made this a private helper method because it’s not very useful outside of a Fraction object. In other words, it’s a method that I’ll only use internally within my Fraction class. Once we have this method, reducing a Fraction object is very simple:

    public void reduce() {
        int greatestCommonFactor = gcd( num, den );
        num = num / greatestCommonFactor;
        den = den / greatestCommonFactor;        
    }

public void reduce() {

int greatestCommonFactor = gcd( num, den );

num = num / greatestCommonFactor;

den = den / greatestCommonFactor;

}

Using this method we can now reduce Fraction objects:

> Fraction f = new Fraction( 90, 144 )
> System.out.println( f )
90/144
> f.reduce( )
> System.out.println( f )
5/8

Adding Fraction Objects

Adding, subtracting, multiplying, and dividing fractions are all very useful operations. Let’s implement a method to add the current Fraction object to some other (parameter) Fraction object, and return a reference to a new Fraction object that is the sum.

    public Fraction add( Fraction other ) {
        int newNum =  num * other.getDen() + other.getNum() * den;
        int newDen =  den * other.getDen();
        // Create a new Fraction object for sum, reduce it, then return a reference to it
        Fraction sum = new Fraction( newNum, newDen );     
        sum.reduce();
        return sum; 
    }

public Fraction add( Fraction other ) {

int newNum = num * other.getDen() + other.getNum() * den;

int newDen = den * other.getDen();

// Create a new Fraction object for sum, reduce it, then return a reference to it

Fraction sum = new Fraction( newNum, newDen );

sum.reduce();

return sum;

}

In case you’ve forgotten, the formula for adding fractions is: If you look at the method signature above you’ll see that the return type is Fraction. This means that the method must return a reference to a Fraction object.

Line 2 uses the num and den of the current Fraction object and uses the accessor methods of the other (parameter) Fraction object to calculate the numerator of the new (sum) Fraction object instantiated on line 4. Similarly, line 3 calculates the new denominator.

The local variable sum refers to the new Fraction object that is the sum of the current Fraction object and its other parameter. On line 6 we call the reduce() method of this new Fraction object, before returning a reference to it on line 7.

Here’s an interaction with this new method:

> Fraction f1 = new Fraction( 8, 18 )
> Fraction f2 = new Fraction( 2, 6 )
> Fraction f3 = f1.add( f2 )
> System.out.println( f3 )
7/9

As the designer of the Fraction class you might decide that the add() method would make a good candidate for a static method:

    public static Fraction add( Fraction f1, Fraction f2 ) {
        int newNum =  f1.getNum() * f2.getDen() + f2.getNum() * f1.getDen();
        int newDen =  f1.getDen() * f2.getDen();
        Fraction sum = new Fraction( newNum, newDen );
        sum.reduce();
        return sum; 
    }

public static Fraction add( Fraction f1, Fraction f2 ) {

int newNum = f1.getNum() * f2.getDen() + f2.getNum() * f1.getDen();

int newDen = f1.getDen() * f2.getDen();

Fraction sum = new Fraction( newNum, newDen );

sum.reduce();

return sum;

}

This is very similar to our previous add() method except this one accepts two parameters, both references to a Fraction object. As before it creates a new Fraction object sum and returns a reference to it. Because it’s a static method we can call it using the Fraction class name. Here’s a sample interaction:

> Fraction f1 = new Fraction( 8, 18 )
> Fraction f2 = new Fraction( 2, 6 )
> Fraction f3 = Fraction.add( f1, f2 )
> System.out.println( f3 )
7/9

Pass-by-Copy with Object References

In 2-1 we talked about pass-by-copy with primitive-type arguments. You will recall that with a primitive variable, a copy of the data stored in the variable was passed as an argument. As a result, any change to the parameter within the method had no effect on the original data passed in. Pass-by-copy also applies when we give an object reference variable as an argument to a method, but there is an important difference!

When an object reference is passed as an argument, a copy of the reference (i.e., memory location) is passed as an argument not a copy of the actual object. This means that both the calling code and the method will be referring to the same object in memory. Any change made to the object in the method (e.g., by calling a mutator) will change the object referred to by the calling code as well. Consider the following code:

public class FractionTest {
    public static void main(String[] args) {
        Fraction f1 = new Fraction(4,6);
        System.out.println( "Fraction object from main(): " + f1);
        objectRefDemo( f1 );
        System.out.println( "Fraction object from main(): " + f1);       
    }
    
    public static void objectRefDemo( Fraction f2 ) {
        System.out.println( "Fraction object from objectRefDemo(): " + f2) ;
        f2.reduce();
        System.out.println( "Fraction object after reduce(): " + f2 );
    }
}

public class FractionTest {

public static void main(String[] args) {

Fraction f1 = new Fraction(4,6);

System.out.println( "Fraction object from main(): " + f1);

objectRefDemo( f1 );

System.out.println( "Fraction object from main(): " + f1);

}

public static void objectRefDemo( Fraction f2 ) {

System.out.println( "Fraction object from objectRefDemo(): " + f2) ;

f2.reduce();

System.out.println( "Fraction object after reduce(): " + f2 );

}

Fraction object from main(): 4/6
Fraction object from objectRefDemo(): 4/6
Fraction object after reduce(): 2/3
Fraction object from main(): 2/3

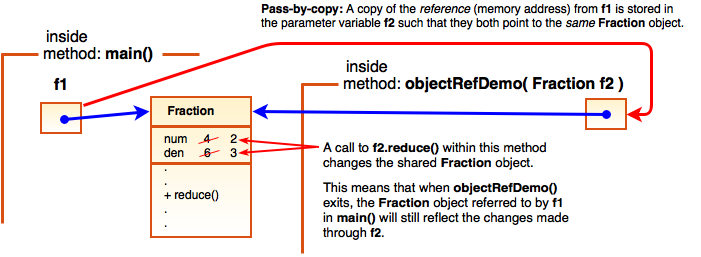
On line 3 we instantiate a Fraction object, and the f1 reference variable contains the address of this object in memory. On line 5 we call the objectRefDemo() method and provide f1 as an argument. Because f1 is a reference-type, what the objectRefDemo() method receives in its f2 parameter is a copy of the memory address stored in f1.

Now, since both f1 and f2 contain the same memory address, they both refer to the same Fraction object in memory. The call to reduce() on line 11 changes numerator and denominator of this shared Fraction object. Therefore, even after the objectRefDemo() method exits, the changes made to the Fraction object through f2 affect f1 in main().

Here is a diagram to illustrate:

2-9-pass-by-copy

You Try!

Implement a subtract(), multiply(), or divide() instance method (pick one). Write a main() method and test class to demonstrate it.
Implement a subtract(), multiply(), or divide() static class method (pick one). Write a main() method and test class to demonstrate it.
Draw an updated UML diagram for the Fraction class based on all of the new methods added in the notes and Q1 and Q2 above. Remember that private instance variables and methods are always prefaced with the minus (–) sign in UML.
Add a boolean method called isOverlapping() to your Rectangle class that accepts a reference to another Rectangle object as a parameter and determines whether the current Rectangle object overlaps with the parameter Rectangle object.
Our future paint program will also support the drawing of Oval objects. Note that in the case of an Oval, the (x1, y1), and (x2, y2) coordinates will define a rectangular bounding area within which the Oval will be drawn by our paint program.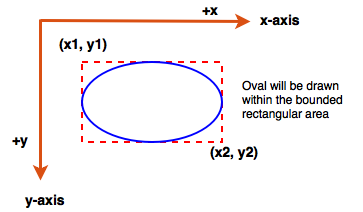Write an Oval class modelled after your Rectangle class. Include the same instance variables (x1, y1, x2, y2, and filled) and methods, excluding the isOverlapping() method. Instead of an isOverlapping() method, write a boolean method called isCircle() that returns true if the current Oval object has its width equal to its height, or false otherwise. Don’t forget to update the calcArea() method for an oval. Here is a UML class diagram for your implementation: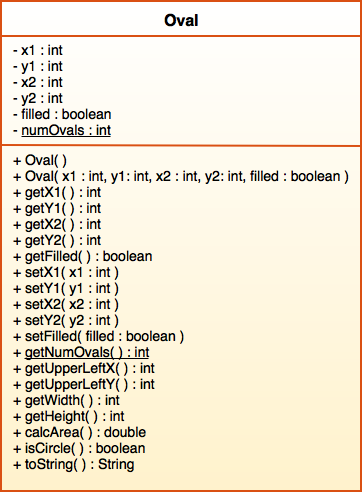You can see that the Oval class is extremely similar to the Rectangle class. We’ll use this similarity to our advantage next time!