2-3 Recursive Methods

In 1-8 to 1-10 we learned about using iteration to repeat a block of code. Another way of repeating code is to create a recursive method. The simple definition of a recursive method is a method that calls itself. Designing such a method takes some careful thought.

Blast-Off!

Consider the following example:

If we call blastOff(3) the output would look like this:

3
2
1
Blast-Off!

In its basic form, a recursive method contains an if..else statement. One clause of the if..else statement is a special case that will cause the recursion to stop; this is called the base case. Our base case here is when ( count == 0 ) we display the “Blast-Off!” message and the method exits using return; This case will cause recursion to stop because the method is not calling itself again, just exiting. Note that the return; statement is actually optional here because the method will terminate naturally after the if..else statement without it – I’ve just included it for clarity.

If the base case is false, then the else clause executes printing the current value of the count parameter, and then calling itself again with the value of count reduced by 1. This is called the recursive case because it does two things: (1) it reduces the complexity of the problem by solving a small part of the problem (i.e., printing one of the count down numbers), and (2) it recursively calls itself again to solve the remainder of the problem (i.e., continuing the count down from the next number). It’s this recursive case that gives us the behavior of repetition without having to use a loop structure.

Method Overhead

The first time blastOff(3) is called is in main(). After that, blastOff() will call itself 3 more times until the base case is executed. Therefore, we say that the depth of recursion (the number of times a method calls itself) is 3 in this example.

When a method calls itself the JVM essentially has to make a new copy of it in memory. So, if we call BlastOff(3) we will eventually have 4 copies of the method in memory at once:

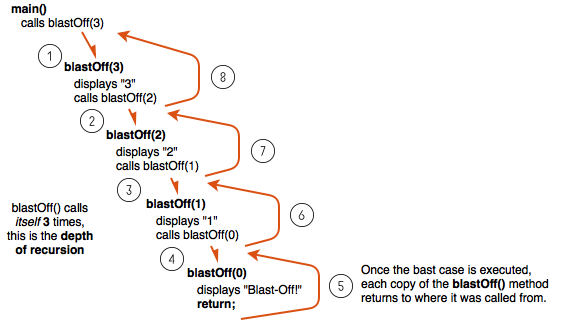2-3-Recursion1Recursion requires a new copy of the method (all its variables and code), to be loaded into memory every time the method is called — we call this overhead. Method overhead is the extra CPU time and system memory needed to manage a method as it runs.

Iteration > Recursion

So, now we have two different ways of repeating code in our programs. Which is better?

In general, iteration is better for 3 main reasons. First, any problem that can be solved recursively can be solved iteratively. As a programmer, one could live very happily without recursive methods, but the opposite cannot be said about loops. Second, loop structures are more efficient than recursive methods because there is no method overhead to worry about.

The third reason is related to the last point above. Recall that a loop that never terminates (usually due to a badly designed loop continuation condition) is called an infinite loop. An infinite loop is rarely desirable but will not normally crash a program – it just keeps iterating the same code block “forever” until you force it to terminate. With a recursive method, if we poorly design our base case, the recursive process will have no way to end. This is called infinite recursion, and it’s a more serious logic problem than an infinite loop because eventually the JVM will run out of memory (due to method overhead) and the program will crash. So, in practice, there is no such thing as truly infinite recursion – it’s going to crash at some depth.

Why Bother with Recursion?

Despite the reasons above, iteration is not always the best choice. Some problems, related to math and algorithms related to searching and sorting, have naturally recursive solutions. In these cases, while an iterative solution is possible, a recursive solution results in a program that is shorter, easier to understand, and debug.

Next, we’ll look at two examples from mathematics that are naturally recursive algorithms, and later when we talk about data structures and algorithms we’ll see recursion in action again.

Linear Recursion

Calculating the factorial value of a number (!) is a classic example of a problem that may be solved recursively. Consider:

2-3-Factorial1An important fact to remember about factorials is that 0! = 1.

At this point I’m sure you could easily write an iterative value method that would do the job:

The code above is perfectly acceptable, but let’s think about this problem in a recursive way:
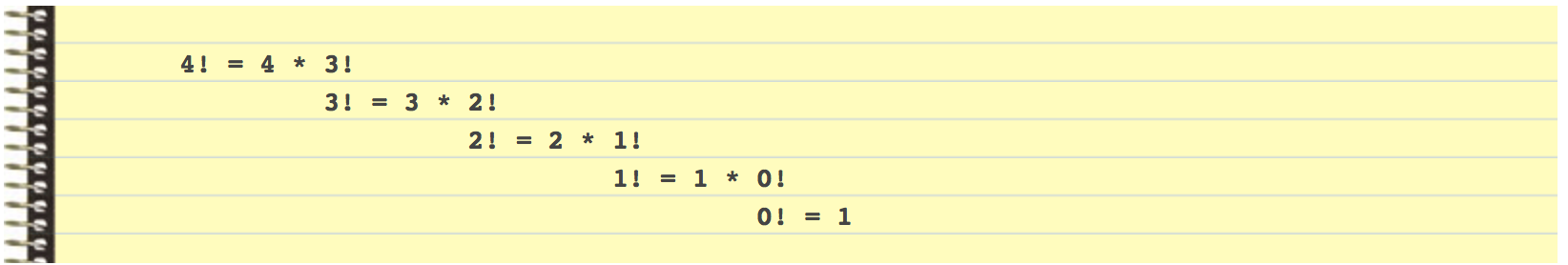2-3-Factorial2We can think of 4! as 4 x 3!. 4 x is part of the overall solution, and 3! is a simpler version of the original problem. We can continue in this way until we get to the base case: 0! = 1 at which point the recursive method calls stop, each method returns its part of the result, and we end up with a final answer of 24.

It turns out that calculating a factorial is a naturally recursive process, in fact it has a (recursive) mathematical definition:

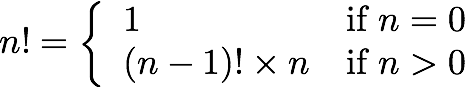2-3-FactorialDefIn this example, the base case comes from the fact that 0! = 1.  The second case is the recursive case. Translating this mathematical definition into a Java method is very straightforward.

This is an example of linear recursion. Linear recursion means that a method calls itself only 1 time during the recursive case. If we call factorial(4), the recursion produces a linear “chain” of method calls like this:

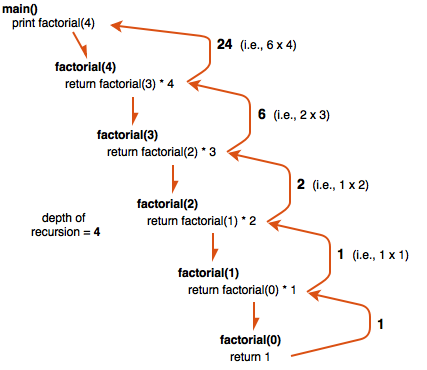At the bottom of the chain, once we hit the base case (0! = 1), the bottom recursiveFactorial() method in the chain returns 1. The second to last returns 1, the third to last 2, the next 6, and finally 24.

When we get into data structures and algorithms later we’ll study a linearly recursive search algorithm called the binary search.

Exponential Recursion

If we have a method where the recursive case causes the method to call itself two or more times it’s called exponential recursion. A good example of this is a recursive method to calculate terms of the Fibonacci sequence. You’ll recall that this famous sequence of numbers goes like this:

2-3-FibonacciThe first number is called “term 0”, the second “term 1” etc.. Beginning with the third number (“term 2”), each number is the sum of the preceding two. This can be expressed recursively:

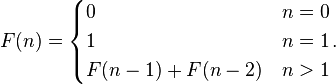2-3-FibonacciDefThere are two interesting things to note here. First, we have 2 base cases. This is not a problem, a recursive method can have any number of base cases as long as it has at least one. Second, the recursive case actually calls itself twice – exponential recursion!  Converting this definition into a Java method is trivial:

If we call fibonacci(4) to calculate term 4 of the sequence, the recursion produces a “tree” of method calls like this:

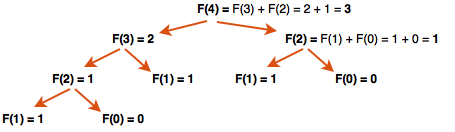2-3-Recursion3We’ll see later how one of the most famous and powerful sorting algorithms (called the quicksort), is an exponentially recursive algorithm.

You Try!

  1. The Greek mathematician Euclid stated one of the most famous recursive functions over 2000 years ago.  Euclid’s algorithm, as it is called, provides a method of finding the greatest common divisor (GCD) of a pair of natural numbers.
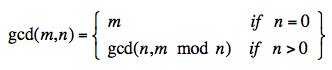    2-3-euclidsalgorithmWrite a recursive method called gcd() and a main() method to demonstrate its use.
  2. In 2-2 Q#1 you created a method called iterativePower() to calculate exponential values.  Now write a recursive version called recursivePower() that takes an integer base and exponent as parameters and returns the base raised to the exponent.  For example, recursivePower( 2, 4 ) should return 16.  Again, do not use any Math class methods.  Write a main() method to demonstrate your method.
  3. Write a recursive method called printDigits() that accepts an integer as a parameter and displays each digit of the integer on a separate line.
  4. Below are six mysterious recursive methods and a main() method to demonstrate them.  Try to analyze each method to determine what they do.  After that, try the code in Dr. Java to see if you are correct.